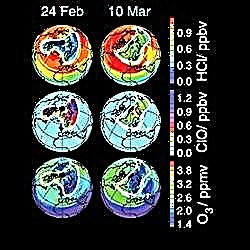
Onderschrift: View of the moon at perigee and apogee
Als docent ben ik altijd op zoek naar labs met eenvoudige instellingen die geschikt zijn voor studenten. Mijn huidige favoriet is het vinden van de lichtsnelheid met chocolade.
In een nieuw artikel dat onlangs is geüpload naar arXiv, beschrijft Kevin Krisciunas uit Texas A&M een methode voor het bepalen van de excentriciteit van de baan van de maan met een verrassend lage fout met niet meer dan een meterstok, een stuk karton en een programma dat bedoeld is om bochten aan te passen aan variabele sterren.
Deze methode maakt gebruik van het feit dat de excentriciteit kan worden bepaald uit de verhouding van de gemiddelde hoekgrootte van een object en de helft van de amplitude. Het belangrijkste doel is dus om deze twee hoeveelheden te meten.
Kevin's strategie om dit te doen is om gebruik te maken van een kartonnen kijkgat dat langs een meterstok kan glijden. Door door het gat bij de maan te turen en de kaart heen en weer te schuiven totdat de hoekgrootte van het gat de maan net overlapt. Van daaruit geeft de diameter van het gat gedeeld door de afstand langs de meterstok de hoekmaat dankzij de kleine hoekformule (? = D / D in radialen als D >> d).
Om systematische verkeerde inschattingen te voorkomen wanneer de kaart naar voren wordt geschoven totdat de grootte van het gat overeenkomt met de maan, is het het beste om het ook vanuit de andere richting te benaderen; Komt van binnenuit vanaf het uiteinde van de meterstok. Dit zou fouten moeten helpen verminderen en bij Kevin's poging ontdekte hij dat hij daarbij een typische spreiding van ± 4 mm had.
Op dit punt is er nog een andere systematische fout waarmee rekening moet worden gehouden: de pupil heeft een eindige grootte die vergelijkbaar is met het kijkgat. Hierdoor wordt de werkelijke hoekmaat onderschat. Als zodanig is een correctiefactor nodig.
Om deze correctiefactor af te leiden, plaatste Kevin een schijf van 91 mm op een afstand van 10 meter (dit zou een schijf moeten opleveren met dezelfde hoekgrootte als de maan gezien vanaf die afstand). Om de beste match te maken, het stuk karton met het kijkgat zou moeten moet op 681,3 mm op de meterstok worden geplaatst, maar vanwege de systematische fout van de pupil vond Kevin dat deze op 821 mm moest worden geplaatst. De verhouding tussen de waargenomen plaatsing en de juiste plaatsing leverde de correctiefactor op die Kevin gebruikte (1.205). Dit zou voor elke individuele persoon moeten worden gekalibreerd en zou ook afhangen van de hoeveelheid licht tijdens de observatieperiode, omdat dit ook de diameter van de pupil beïnvloedt. Het gebruik van een enkele correctiefactor levert echter bevredigende resultaten op.
Dit zorgt voor correct genomen gegevens die vervolgens kunnen worden gebruikt om de benodigde grootheden te bepalen (de gemiddelde hoekgrootte en 1/2 amplitude). Om deze te bepalen, gebruikte Kevin een programma dat bekend staat als PERDET en dat is ontworpen voor het aanpassen van sinusoïde curven aan oscillaties in variabele sterren. Elk programma dat dergelijke krommen zou kunnen aanpassen aan gegevenspunten met behulp van een?2 fit of een Fourier-analyse zou hiervoor geschikt zijn.
Van dergelijke programma's, zodra de gemiddelde hoekgrootte en halve amplitude zijn bepaald, levert hun verhouding de excentriciteit op. Voor Kevin's experiment vond hij een waarde van 0,039 ± 0,006. Bovendien was de periode die hij van perigee tot perigee bepaalde 27,24 ± 0,29 dagen, wat in uitstekende overeenstemming is met de aanvaarde waarde van 27,55 dagen.